解：∵抛物线y=x²-2mx+m²与直线y=2x相交，

∴x²-2mx+m²=2x

∴x²-2（m+1）x+m²=0

∴[-2（m+1）]²-4m²≥0，解得m≥-，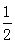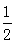

∵m<2，∴-≤m<2

∵m为整数，

∴m=0，1

∵抛物线y=x²-2mx+m²与直线y=2x交点的横坐标均为整数，即方程x²-2mx+m²=2x的根为整数

当m=0时，x²-2x=0，解得x=0或x=2，两根均为整数，m=0符合题意

当m=1时，x²-4x+1=0

∵△=（-4）²-4=12，

∴x²-4x+1=0没有整数根，

∴m=1不符合题意，舍去，

∴满足条件的m的整数值为0。