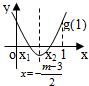已知二次函数f（x）满足f(0)=1，f(1)=-1，f(32+x)=f(32-

问题解答题

已知二次函数f（x）满足f(0)=1，f(1)=-1，f(

+x)=f(

-x)．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若方程f（x）=-mx的两根x₁和x₂满足x₁＜x₂＜1，求实数m的取值范围．

答案

（Ⅰ）设二次函数f（x）=ax²+bx+c，则抛物线的对称轴为x=

．

根据题意得

c=1

a+b+c=-1

，

解之得a=1，b=-3，c=1．

所以，函数f（x）的解析式为f（x）=x²-3x+1．

（Ⅱ）由f（x）=x²-3x+1=-mx得x²+（m-3）x+1=0．

设g（x）=x²+（m-3）x+1，

则抛物线的对称轴为x=-

m-3

．

方程g（x）=0的两根x₁和x₂满足x₁＜x₂＜1，

则有

△=(m-3)2-4＞0

g(1)=m-1＞0

m-3

＜1

解之得m＞5．

所以，实数m的取值范围为（5，+∞）．