问题
填空题
抛物线y=-
|
答案
将抛物线方程化成标准方程为x2=-4y，
可知焦点坐标为（0，-1），-3＜-
，所以点E（1，-3）在抛物线的内部，1 4
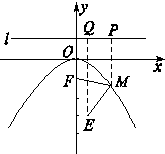
如图所示，设抛物线的准线为l，过M点作MP⊥l于点P，
过点E作EQ⊥l于点Q，由抛物线的定义可知，|MF|+|ME|
=|MP|+|ME|≥|EQ|，当且仅当点M在EQ上时取等号，又
|EQ|=1-（-3）=4，故距离之和的最小值为4．
故答案为：4．
搜题请搜索小程序“爱下问搜题”