问题
填空题
设f（x）=
|
答案
在坐标系中作出函数f(x)=
的图象，x2x≥1或x≤-1 x-1＜x＜1
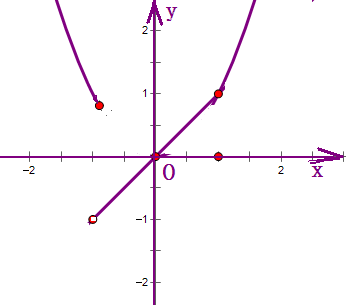
观察图象可知，当纵坐标在[0，+∞）上时，横坐标在（-∞，-1]∪[0，+∞]上变化，
f（x）的值域是（-1，+∞），而f（g（x））的值域是[0，+∞），
∵g（x）是二次函数
∴g（x）的值域是[0，+∞）．
故答案为：[0，+∞）．
搜题请搜索小程序“爱下问搜题”
设f（x）=
|
在坐标系中作出函数f(x)=
的图象，x2x≥1或x≤-1 x-1＜x＜1
观察图象可知，当纵坐标在[0，+∞）上时，横坐标在（-∞，-1]∪[0，+∞]上变化，
f（x）的值域是（-1，+∞），而f（g（x））的值域是[0，+∞），
∵g（x）是二次函数
∴g（x）的值域是[0，+∞）．
故答案为：[0，+∞）．