问题
填空题
过抛物线y2=4x的焦点作直线l,交抛物线于A,B两点,若线段AB中点的横坐标为3,则|AB|等于______.
答案
∵抛物线方程为y2=4x,∴抛物线的焦点为F(1,0),准线为l:x=-1
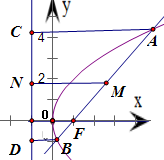
设线段AB的中点为M(3,y0),则M到准线的距离为:|MN|=3-(-1)=4,
过A、B分别作AC、BD与l垂直,垂足分别为C、D
根据梯形中位线定理,可得|AC|+|BD|=2|MN|=8
再由抛物线的定义知:|AF|=|AC|,|BF|=|BD|
∴|AB|=|AF|+|BF||AC|+|BD|=8.
故答案为:8
