问题
填空题
当x∈（3，4）时，不等式x2+mx+4＜0恒成立，则m的取值范围是______．
答案
利用函数f（x）=x2+mx+4的图象，
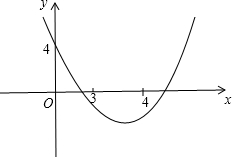
∵x∈（3，4）时，不等式x2+mx+4＜0恒成立，
∴
⇒f(3)≤0 f(4)≤0
⇒m≤-5．m≤- 13 3 m≤-5
故答案是m≤-5．
搜题请搜索小程序“爱下问搜题”
当x∈（3，4）时，不等式x2+mx+4＜0恒成立，则m的取值范围是______．
利用函数f（x）=x2+mx+4的图象，
∵x∈（3，4）时，不等式x2+mx+4＜0恒成立，
∴
⇒f(3)≤0 f(4)≤0
⇒m≤-5．m≤- 13 3 m≤-5
故答案是m≤-5．