问题
解答题
在经济学中，函数f（x）的边际函数为 Mf（x）=f（x+1）-f（x）。某公司每月最多生产100台电子产 品，生产x（x∈[1，100]，x∈N*）台该产品的收入函数为R（x）=3000x-20x2（单位：元），其成本函数为C（x）=500x+4000（单位：元），利润是收入与成本之差。
（1）求利润函数P（x）及边际利润函数MP（x）；
（2）求利润函数P（x）及边际利润函数MP（x）的最大值；
（3）你认为本题中边际利润函数MP（x）取最大值的实际意义是什么？
答案
解：（1）依题意，得P（x）=R（x）-C（x）=-20x2+2500x-4000（x∈[1，100]，x∈N*）；
MP（x）=P（x+1）-P（x）=-40x+2480（x∈[1，100]，x∈N*）。
（2）由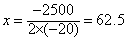
，且x∈N*，得x=62或x=63时，P（x）max=74120（元）；
当x=1时，MP（x）max=2440（元）。
（3）当x=1时，边际利润函数MP（x）取得最大值，说明生产2台与生产1台的利润差最大，又P（1）＜MP（1），故生产第2台电子产品的利润最大，由MP（x）=-40x+2480是减函数知随着产量的增加，每台利润与前一台利润的差在减小。