问题
解答题
在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x)。某公司每月生产x台,某种产品的收入为R(x)元,成本为C(x)元,且R(x)= 3000x-20x2,C(x)=500x+4000(x∈N*)。现已知该公司每月生产该产品不超过100台。
(1)求利润函数P(x)以及它的边际利润函数MP(x);
(2)求利润函数的最大值与边际利润函数的最大值之差。
答案
解:(1)由题意得,x∈[1,100],且x∈N*
P(x)=R(x)-C(x)=(3000x-20x2)-(500x+4000)
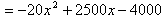
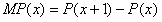
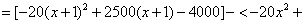

=2480-40x。
(2)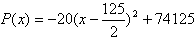
当x=62,或x=63时,P(x)的最大值为74120(元);
因为MP(x)=2480-40x是减函数,
所以当x=1时,MP(x)的最大值为2440(元)
故利润函数的最大值与边际利润函数的最大值之差为71680元。
