问题
解答题
已知抛物线x2=4y,点P是抛物线上的动点,点A的坐标为(12,6),求点P到点A的距离与到x轴的距离之和的最小值.
答案
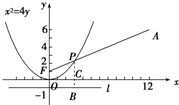
将x=12代入x2=4y,得y=36>6,
所以点A在抛物线外部.抛物线焦点为F(0,1),准线l:y=-1.
如图所示,过P点作PB⊥l于点B,交x轴于点C,
则PA+PC=PA+PB-1=PA+PF-1.
由图可知,当A、P、F三点共线时,PA+PF的值最小,
所以PA+PF的最小值为FA=13,
故PA+PC的最小值为12.
