(1) 证明略，(2)证明略(3) f(x)=2x²－1

 由条件当=1≤x≤1时，|f(x)|≤1，

取x=0得 |c|=|f(0)|≤1，即|c|≤1 

(2)证法一： 依题设|f(0)|≤1而f(0)=c，

所以|c|≤1。 当a＞0时，g(x)=ax+b在［－1，1］上是增函数，

于是g(－1)≤g(x)≤g(1)，(－1≤x≤1)。 

∵|f(x)|≤1，(－1≤x≤1)，|c|≤1，

∴g(1)=a+b=f(1)－c≤|f(1)|+|c|=2，

g(－1)=－a+b=－f(－1)+c≥－(|f(－2)|+|c|)≥－2，

因此得|g(x)|≤2  (－1≤x≤1)；

当a＜0时，g(x)=ax+b在［－1，1］上是减函数，

于是g(－1)≥g(x)≥g(1)，(－1≤x≤1)，

∵|f(x)|≤1  (－1≤x≤1)，|c|≤1

∴|g(x)|=|f(1)－c|≤|f(1)|+|c|≤2。

综合以上结果，当－1≤x≤1时，都有|g(x)|≤2。

证法二：∵|f(x)|≤1(－1≤x≤1)

∴|f(－1)|≤1，|f(1)|≤1，|f(0)|≤1，

∵f(x)=ax²+bx+c，∴|a－b+c|≤1，|a+b+c|≤1，|c|≤1，

因此，根据绝对值不等式性质得：

|a－b|=|(a－b+c)－c|≤|a－b+c|+|c|≤2，

|a+b|=|(a+b+c)－c|≤|a+b+c|+|c|≤2，

∵g(x)=ax+b，∴|g(±1)|=|±a+b|=|a±b|≤2，

函数g(x)=ax+b的图象是一条直线，

因此|g(x)|在［－1，1］上的最大值只能在区间的端点x=－1或x=1处取得，于是由|g(±1)|≤2得|g(x)|≤2，(－1＜x＜1。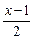

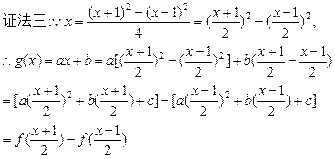
当－1≤x≤1时，有0≤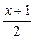≤1，－1≤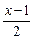≤0，

∵|f(x)|≤1，(－1≤x≤1)，∴|f 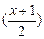|≤1，|f(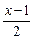)|≤1；

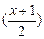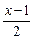因此当－1≤x≤1时，|g(x)|≤|f |+|f()|≤2。

(3)解： 因为a＞0，g(x)在［－1，1］上是增函数，当x=1时取得最大值2，即g(1)=a+b=f(1)－f(0)=2。                             ①

∵－1≤f(0)=f(1)－2≤1－2=－1，∴c=f(0)=－1。

因为当－1≤x≤1时，f(x)≥－1，即f(x)≥f(0)，

根据二次函数的性质，直线x=0为f(x)的图象的对称轴，

由此得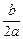－＜0 ，即b=0。

由①得a=2，所以f(x)=2x²－1。