等差数列{an}的公差和等比数列{bn}的公比都是d（d≠1），且a1=b1，a

问题解答题

等差数列{a_n}的公差和等比数列{b_n}的公比都是d（d≠1），且a₁=b₁，a₄=b₄，a₁₀=b₁₀．

（1）求实数a₁和d的值；

（2）b₁₆是不是{a_n}中的项？如果是，是第几项？如果不是，请说明理由．

答案

(1)a_n=a₁+(n-1)d，b_n=b₁q^n-1=a₁d^n-1．

由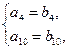得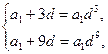

即．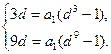

两式相除整理得d⁹+3d³+2=0．

解得d³=-2或d³=1（舍去）．

∴d=-．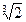

代入原方程中得a₁=．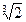

∴a₁=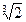，d=-．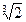

(2)由(1)得数列{a_n}、{b_n}的通项分别为

a_n=(2-n)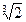，b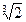_n=-(-)ⁿ．

故b₁₆=-(-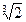)¹⁶=-32．

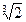由(2-n)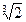=-32，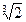

解得n=34．

故b₁₆是数列{a_n}中的第34项.

根据题设可知本题的等差数列、等比数列中的各项都能用a₁和d表示，从而可建立起关于a₁和d的方程组，可解出a₁和d．