问题
解答题
设y=(log2x)2+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,求x的取值范围.
答案
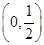 ∪(8,+∞)
∪(8,+∞)
解:设y=f(t)=(log2x-1)t+(log2x)2-2log2x+1,
则f(t)是一次函数,当t∈[-2,2]时,
f(t)>0恒成立,则有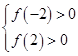
即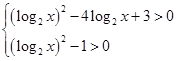
解得log2x<-1或log2x>3.
∴0<x<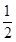 或x>8,
或x>8,
∴x的取值范围是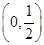 ∪(8,+∞).
∪(8,+∞).
设y=(log2x)2+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,求x的取值范围.
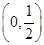 ∪(8,+∞)
∪(8,+∞)
解:设y=f(t)=(log2x-1)t+(log2x)2-2log2x+1,
则f(t)是一次函数,当t∈[-2,2]时,
f(t)>0恒成立,则有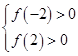
即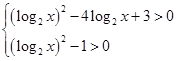
解得log2x<-1或log2x>3.
∴0<x<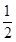 或x>8,
或x>8,
∴x的取值范围是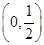 ∪(8,+∞).
∪(8,+∞).