问题
填空题
已知函数f(x)＝mx2－mx－1.若对于x∈R，f(x)＜0恒成立，则实数m的取值范围为 。
答案
-4＜m≤0
题目分析：当m=0时，函数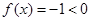
恒成立，所以符合要求；当
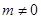时，要使对于x∈R，f(x)＜0恒成立，需要满足
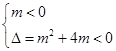，解得
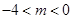，综上可得实数m的取值范围为-4＜m≤0.
点评：考查函数时，不要想当然的认为是二次函数，不要忘记讨论二次项系数为0的情况.
搜题请搜索小程序“爱下问搜题”
已知函数f(x)＝mx2－mx－1.若对于x∈R，f(x)＜0恒成立，则实数m的取值范围为 。
-4＜m≤0
题目分析：当m=0时，函数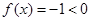恒成立，所以符合要求；当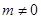时，要使对于x∈R，f(x)＜0恒成立，需要满足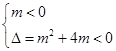，解得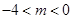，综上可得实数m的取值范围为-4＜m≤0.
点评：考查函数时，不要想当然的认为是二次函数，不要忘记讨论二次项系数为0的情况.