问题
解答题
设f(x)是定义在[-1,1]上的奇函数,且当-1≤x≤0时,f(x)=2x3+5ax2+4a2x+b。
(1)求函数f(x)的解析式;
(2)当1<a≤3时,求函数f(x)在(0,1]上的最大值g(a);
(3)如果对满足1<a≤3的一切实数,函数f(x)在(0,1]上恒有f(x)≤0,求实数b的取值范围。
答案
解:(1)当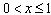 时,
时,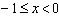 ,则
,则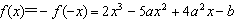
当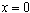 时,
时,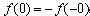
∴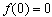
∴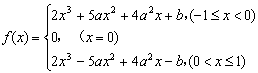 ;
;
(2)当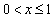 时,
时,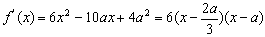
①若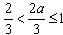 ,即
,即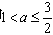
则当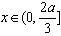 时,
时,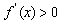 ;
;
当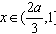 时,
时,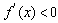
∴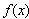 在
在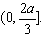 上单调递增,在
上单调递增,在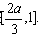 上单调递减
上单调递减
∴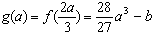
②若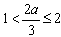 时,即
时,即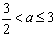
则当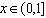 时,
时,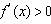
∴f(x)在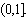 上单调递增
上单调递增
∴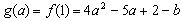
∴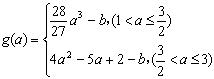 ;
;
(3)要使函数f(x)在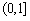 上恒有
上恒有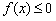 ,必须使
,必须使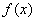 在
在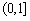 上的最大值
上的最大值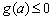 。
。
即对满足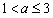 的实数a,
的实数a,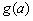 的最大值要小于或等于0
的最大值要小于或等于0
①当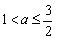 时,
时,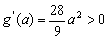 ,此时
,此时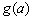 在
在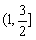 上是增函数
上是增函数
则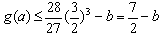
由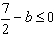
解得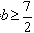
②当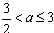 时,
时,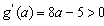 ,此时
,此时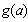 在
在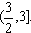 上是增函数
上是增函数
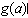 的最大值是
的最大值是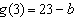
∴由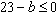
解得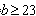
综上,b的取值范围是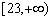 。
。

