问题
解答题
已知a∈R,函数f(x)=x|x-a|,
(Ⅰ)当a=2时,写出函数y=f(x)的单调递增区间;
(Ⅱ)当a>2时,求函数y=f(x)在区间[1,2]的最小值。
答案
解:(Ⅰ)当a=2时,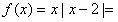
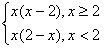 ,
,
由图象可知,单调递增区间为(-∝,1],[2,+∝)。
(Ⅱ)因为a>2,x∈[1,2]时,
所以,f(x)=x(a-x)=-x2+ax=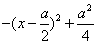 ,
,
当 ,即2<a≤3时,
,即2<a≤3时,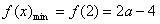 ;
;
当 ,即a>3时,
,即a>3时, ;
;
∴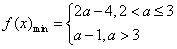 。
。
已知a∈R,函数f(x)=x|x-a|,
(Ⅰ)当a=2时,写出函数y=f(x)的单调递增区间;
(Ⅱ)当a>2时,求函数y=f(x)在区间[1,2]的最小值。
解:(Ⅰ)当a=2时,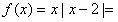
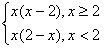 ,
,
由图象可知,单调递增区间为(-∝,1],[2,+∝)。
(Ⅱ)因为a>2,x∈[1,2]时,
所以,f(x)=x(a-x)=-x2+ax=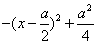 ,
,
当 ,即2<a≤3时,
,即2<a≤3时,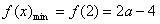 ;
;
当 ,即a>3时,
,即a>3时, ;
;
∴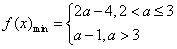 。
。