问题
解答题
作出函数f(x)=|x-2|-|x+1|的图象,并由图象求f(x)的值域.
答案
解:当x<-1时,f(x)=-(x-2)-[-(x+1)]=3;
当-1≤x≤2时, f(x)=-(x-2)-(x+1)=-2x+1;
当x>2时,f(x)=(x-2)-(x+1)=-3,
∴f(x)=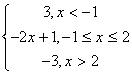 ,
,
f(x)的图象如下图所示,
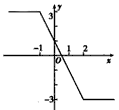
由函数图象知,函数的值域为[-3,3]。
作出函数f(x)=|x-2|-|x+1|的图象,并由图象求f(x)的值域.
解:当x<-1时,f(x)=-(x-2)-[-(x+1)]=3;
当-1≤x≤2时, f(x)=-(x-2)-(x+1)=-2x+1;
当x>2时,f(x)=(x-2)-(x+1)=-3,
∴f(x)=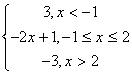 ,
,
f(x)的图象如下图所示,

由函数图象知,函数的值域为[-3,3]。