问题
解答题
求下列函数的单调区间．
(1)f(x)=3|x|；
(2)f(x)=|x2+2x-3|。
答案
解：(1)∵f(x)=3|x|=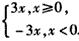
，图象如下图所示，
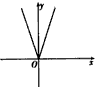
f(x)在(-∞，0]上是减函数，在[0，+∞)上是增函数．
(2)令f(x)=x2+2x-3=(x+1)2-4，先作出f(x)的图象，保留其在x轴及x轴上方部分，把它在x轴下方的图象翻到x轴上方就得到y=|x2+2x-3|的图象，如下图所示，
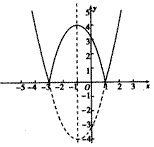
由图象易得：函数的递增区间是[-3，-1]，[1，+∞)；函数的递减区间是(-∞，-3]，[-1，1]．
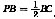