解：由绝对值的几何意义联想到求距离的最小值，如|x-a| +|x-b|的最小值应该是在数轴上a，b两点之间取得，为|a-b|

所以将函数f（x）的右边整理为

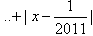
共有1+2+3+…+2011=1006×2011项，则f（x）可以理解为x 到这1006×2011个点的距离之和

从两端开始向中间靠拢，每两个绝对值和的最小值都是在相应的零点之间取得，而且范围是包含关系，比如的最小值是在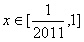上取得

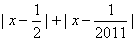的最小值是在

所以，f（x）的最小值应该在正中间的某个零点或相邻两个零点之间取得

由可知取得最小值的范围在第503×2011个零点和第503×2011+1个零点之间（这两个零点也可能相等）

由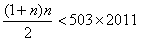算得n≤1421，

所以第503×2011个零点和第503×2011+1个零点均为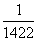

则。