问题
选择题
设△ABC的三内角A、B、C成等差数列，sinA 、sinB、 sinC成等比数列，则这个三角形的形状是（ ）
A．直角三角形 B. 钝角三角形
C．等腰直角三角形 D．等边三角形
答案
答案：D
解：∵△ABC的三内角A、B、C成等差数列，
∴∠B=60°，∠A+∠C=120°①；
又sinA、sinB、sinC成等比数列，
∴sin2B=sinA•sinC=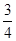
，②由①②得：sinA•sin（120°-A）=sinA•（sin120°cosA-cos120°sinA）=,
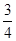∴sin（2A-30°）=1，又0°＜∠A＜120°∴∠A=60°．故选D
