问题
解答题
已知数列{an},a1=2a+1(a≠-1的常数),an=2an-1+n2-4n+2(n≥2,n∈N∗),数列{bn}的首项, b1=a,bn=an+n2(n≥2,n∈N∗).
(1)证明:{bn}从第2项起是以2为公比的等比数列并求{bn}通项公式;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;(3)当a>0时,求数列{an}的最小项.
答案
解：（1）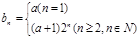
；（2）
。
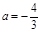（3）当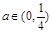
时，最小项为8a-1； 当
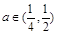时，最小项为4a；当
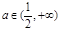时，最小项为2a+1。 当
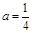时，最小项为4a或8a-1当
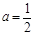时，最小项为4a或2a+1；
bn=an+n2
所以构造出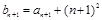
，化简成与bn的代数式；
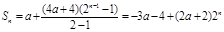是等比数列，∴3a+4=0；
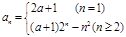分类讨论，an单调性
解：
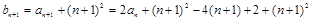
(n≥2)
，∵
,
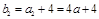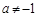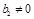,即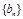
从第2项起是以2为公比的等比数列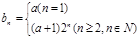
（2）由（1）求得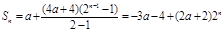
∵
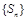是等比数列, ∴3a+4=0，即 。
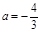（3）由已知当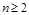
时，
，所以,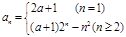
所以数列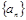
为2a+1，4a，8a-1，16a，32a+7，显然最小项是前三项中的一项。
当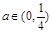时，最小项为8a-1； 当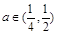时，最小项为4a；当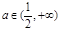时，最小项为2a+1。
当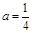时，最小项为4a或8a-1当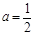时，最小项为4a或2a+1；
