问题
解答题
求函数f(x)=-x2+|x|的单调区间,并求函数y=f(x)在[-1,2]上的最大、小值.
答案
解:①∵f(x)=-x2+|x|=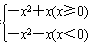 ,
,
即f(x)=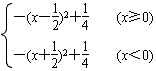 ,
,
作出其在[-1,2]上的图象如右图所示,
由图象可知,f(x)的递增区间为(-∞,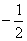 )和[0,
)和[0, ],
],
递减区间为[ ,0]和[
,0]和[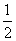 ,+∞);
,+∞);
②由图象知:当x=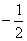 或
或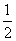 时,f(x)max=
时,f(x)max= ;
;
当x=2时,f(x)min=-2。
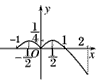
求函数f(x)=-x2+|x|的单调区间,并求函数y=f(x)在[-1,2]上的最大、小值.
解:①∵f(x)=-x2+|x|=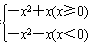 ,
,
即f(x)=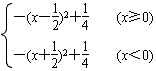 ,
,
作出其在[-1,2]上的图象如右图所示,
由图象可知,f(x)的递增区间为(-∞,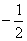 )和[0,
)和[0, ],
],
递减区间为[ ,0]和[
,0]和[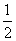 ,+∞);
,+∞);
②由图象知:当x=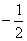 或
或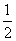 时,f(x)max=
时,f(x)max= ;
;
当x=2时,f(x)min=-2。
