问题
解答题
已知函数f(x)=|x-3|-2，g(x)=-|x+1|+4，
（1）若函数f(x)的值不大于1，求x的取值范围；
（2）若函数f(x)-g(x)≥m+1的解集为R，求m的取值范围。
答案
解：(1)由题意得f(x)≤1，即|x-3|-2≤1得|x-3|≤3，
因为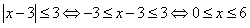
，
所以x的取值范围是[0，6]；
(2)f(x)-g(x)=|x-3|+|x+1|-6，
因为
，由绝对值的三角不等式得
f(x)-g(x)=|x-3|+|x+1|-6
=
，
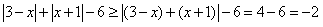于是有m+1≤-2，得m≤-3，
即m的取值范围是(-∞，-3]。