问题
解答题
已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N*),在数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(1)求数列{an},{bn}的通项公式;
(2)记Tn=a1b1+a2b2+ +anbn,求Tn.
答案
(1)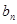 =2n-1;(2)
=2n-1;(2)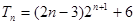 .
.
题目分析:(1)利用“当n=1,a1=2;当n≥2时,an=Sn-Sn-1”和等比数列的通项公式即可得出an;利用等差数列的定义和通项公式即可得出bn.
(Ⅱ)先把所求结论代入求出数列{cn}的通项,再利用数列求和的错位相减法即可求出其各项的和.
试题解析:解(1)由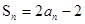 ,得
,得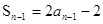 (n≥2)
(n≥2)
两式相减得 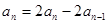 即
即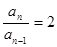 (n≥2)
(n≥2)
又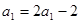 ,∴
,∴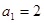
∴{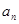 }是以2为首项,以2为公比的等比数列 ∴
}是以2为首项,以2为公比的等比数列 ∴
∵点P( 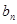 ,
,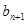 )在直线x-y+2=0上
)在直线x-y+2=0上
∴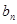 -
- 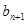 +2="0" 即
+2="0" 即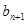 -
-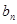 =2
=2
∴{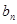 }是等差数列,∵
}是等差数列,∵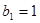 ∴
∴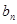 =2n-1
=2n-1
(2) ∵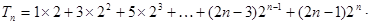
∴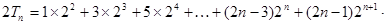
两式相减得,
-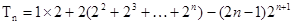
=2+2·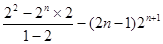
=2+4·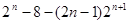
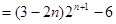
∴