问题
解答题
某旅游点有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元．根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超过6元，则每超过1元，租不出去的自行车就增加3辆，为了便于结算，每辆自行车的日租金x(元)只取整数，并且要求出租自行车一日的总收入必须高于这一日的管理费用，用y (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)，
(1)求函数f(x)的解析式及其定义域；
(2)试问当每辆自行车的日租金定为多少元时，才能使一日的净收入最多？
答案
解：(1)当x≤6时，y=50x-115，令50x-115＞0，解得x＞2.3，
∵x∈N*，
∴x≥3，∴3≤x≤6，x∈N*，
当x＞6时，y=[50-3(x-6)]x-115，
令[50-3(x-6)]x-115＞0，有3x2-68x+115＜0，
上述不等式的整数解为2≤x≤20(x∈N*)，
∴6＜x≤20(x∈N*)，
故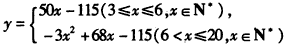
，定义域为{x|3≤x≤20，x∈N*}；
(2)对于y=50x-115（3≤x≤6，x∈N*），显然当x=6时，ymax=185 （元），
对于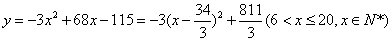
，
当x=11时，ymax=270（元），
∵270＞185，
∴当每辆自行车的日租金定为11元时，才能使一日的净收入最多．