问题
解答题
在数列{an}中，a1＝2，an＋1＝4an－3n＋1，n∈N*.
(1)求证：数列{an－n}是等比数列；
(2)求数列{an}的前n项和Sn；
(3)求证：不等式Sn＋1≤4Sn对任意n∈N*皆成立．
答案
（1）见解析（2）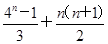
（3）见解析
(1)证明：由题设an＋1＝4an－3n＋1，得an＋1－(n＋1)＝4(an－n)，n∈N*.又a1－1＝1，所以数列{an－n}是首项为1，公比为4的等比数列．
(2)解：由(1)可知an－n＝4n－1，于是数列{an}的通项公式为an＝4n－1＋n，所以数列{an}的前n项和Sn＝.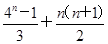
(3)证明：对任意的n∈N*，Sn＋1－4Sn＝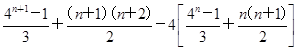
＝－
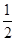(3n2＋n－4)≤0，所以不等式Sn＋1≤4Sn对任意n∈N*皆成立．