问题
解答题
定义在R上的单调函数f(x)满足f(3)=log23且对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求证f(x)为奇函数;
(2)若f(k·3x)+f(3x﹣9x﹣2)<0对任意x∈R恒成立,求实数k的取值范围.
答案
解:(1)证明:f(x+y)=f(x)+f(y)(x,y∈R),①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即f(0)=0.
令y=﹣x,代入①式,得f(x﹣x)=f(x)+f(﹣x),
又f(0)=0,则有0=f(x)+f(﹣x).
即f(﹣x)=﹣f(x)对任意x∈R成立,
所以f(x)是奇函数.
(2)解:f(3)=log23>0,即f(3)>f(0),
又f(x)在R上是单调函数,所以f(x)在R上是增函数,
又由(1)f(x)是奇函数.
f(k·3x)<﹣f(3x﹣9x﹣2)=f(﹣3x+9x+2),
k·3x<﹣3x+9x+2,
令t=3x>0,分离系数得: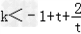 ,
,
问题等价于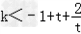 ,
,
对任意t>0恒成立.
∵ ,
,
∴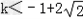 .
.
