问题
填空题
设y＝f(x)是一次函数，f(0)＝1，且f(1)，f(4)，f(13)成等比数列，则f(2)＋f(4)＋…＋f(2n)＝________.
答案
n(2n＋3)
设f(x)＝kx＋b(k≠0)，又f(0)＝1，所以b＝1，即f(x)＝kx＋1(k≠0)．由f(1)，f(4)，f(13)成等比数列，得f2(4)＝f(1)·f(13)，即(4k＋1)2＝(k＋1)(13k＋1)．因为k≠0，所以k＝2，所以f(x)＝2x＋1，所以f(2)＋f(4)＋…＋f(2n)＝5＋9＋…＋4n＋1＝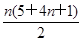
＝n(2n＋3)．