已知函数f（x）对任意x，y∈R，满足条件f（x）+f（y）=2+f（x+y），

问题解答题

已知函数f（x）对任意x，y∈R，满足条件f（x）+f（y）=2+f（x+y），且当x＞0时，

f（x）＞2，f（3）=5．

（1）判断函数f（x）的单调性；

（2）求不等式f（a²﹣2a﹣2）＜3的解集．

答案

解：（1）设x₁＜x₂，则x₂﹣x₁＞0，

∵x＞0，f（x）＞2；

∴f（x₂﹣x₁）＞2；

即f（x₂）=f[（_x2﹣x₁）+x₁]=f（x₂﹣x₁）+f（x₁）﹣2＞2+f（x₁）﹣2=f（x₁），

即f（x₂）＞f（x₁）．

所以：函数f（x）为单调增函数

（2）∵f（3）=f（2+1）=f（2）+f（1）﹣2=[f（1）+f（1）﹣2]+f（1）﹣2=3f（1）﹣4=5

∴f（1）=3．即f（a²﹣2a﹣2）＜3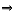f（a²﹣2a﹣2）＜f（1）

∴a²﹣2a﹣2＜1a²﹣2a﹣3＜0

解得不等式的解为：﹣1＜a＜3．