阅读理解。
John sent for a doctor because his wife was ill. He called the doctor and made sure they would meet
at five. He arrived at the doctor's at twenty to five. He thought," It's a little bit earlier. I'll wait for a
moment. It's good to keep the time."
Then he stopped his car in front of the doctor's. He looked around and saw a noisy square (厂场)
not far from here. He went there and sat down on a chair to enjoy the last light of afternoon sun and
make himself quiet. He saw some children playing and some women talking to each other happily.
Suddenly he heard a girl crying. He came up to her and asked some questions. Then he knew she
got lost. John tried to find out her address and took her home. The girl's parents were very thankful.
Then John hurried to the doctor's. The doctor said angrily when he saw him, "You're late. Why did
you keep me waiting for twenty minutes?" John said nothing but one word "Sorry! "
l. John drove to the doctor's _____.
A. late
B. on time
C. in time
D. in no time
2. John went to the square to _____.
A. spend the time
B. enjoy himself
C. see the children and the women
D. help the girl
3. The girl cried because _____.
A. someone hit her
B. she fell off her bike
C. her parents were angry with her
D. she didn't find the way home
4. At last John got to the doctor's at _____.
A. twenty to five
B. twenty past five
C. five o'clock
D. forty past five
5. From the story, we know John is a _____.
A. busy person
B. quiet person
C. helpful person
D. lucky person
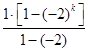 =
= ,Sk+1=
,Sk+1= ,Sk+2=
,Sk+2=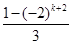 ,
, +
+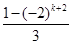 =
= =
=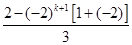 =
=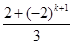 =2·
=2· =2Sk.
=2Sk.