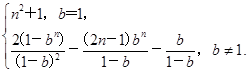已知数列{an}的前n项和Sn＝n2＋1，数列{bn}是首项为1，公比为b的等比

问题解答题

已知数列{a_n}的前n项和S_n＝n²＋1，数列{b_n}是首项为1，公比为b的等比数列．

(1)求数列{a_n}的通项公式；

(2)求数列{a_nb_n}的前n项和T_n.

答案

(1) a_n＝(2) T_n＝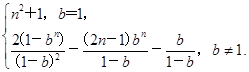

(1)当n＝1时，a₁＝S₁＝2；当n≥2时，a_n＝S_n－S_n_－1＝n²＋1－(n－1)²－1＝2n－1.

所以a_n＝

(2)当b＝1时，a_nb_n＝

此时，T_n＝2＋3＋5＋…＋(2n－1)＝n²＋1.

当b≠1时，a_nb_n＝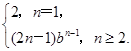

此时，T_n＝2＋3b＋5b²＋…＋(2n－1)bⁿ^－1，①

两端同时乘以b，得bT_n＝2b＋3b²＋5b³＋…＋(2n－1)bⁿ.②

①－②，得(1－b)T_n＝2＋b＋2b²＋2b³＋…＋2bⁿ^－1－(2n－1)bⁿ＝

2(1＋b＋b²＋b³＋…bⁿ^－1)－(2n－1)·bⁿ－b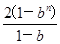＝－(2n－1)bⁿ－b，所以T_n＝－.

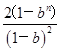综上所述，T_n＝