问题
解答题
设集合Pn={1,2,…,n},n∈N*,记f(n)为同时满足下列条件的集合A的个数:
①A?Pn;②若x∈A,则2x?A;③若x∈A,则2x? A。
(1)求f(4);
(2)求f(n)的解析式(用n表示)。
答案
解(1)当n=4时,P4={1,2,3,,4},符合条件的集合A为:{2},{1,4},{2,3},{1,3,4}
故f(4)=4。
(2)任取偶数x∈Pn,将x除以2,若商仍为偶数,再除以2…,经过k次后,商必为奇数,此时记商为m,于是x=m?2k,其中m为奇数,k∈N*
由条件可知,若m∈A,则x∈A,?k为偶数
若m?A,则x∈A?k为奇数
于是x是否属于A由m是否属于A确定,
设Qn是Pn中所有的奇数的集合
因此f(n)等于Qn的子集个数,当n为偶数时(或奇数时),Pn中奇数的个数是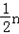 (或
(或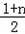 )
)
∴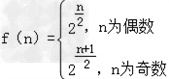 。
。
