问题
选择题
已知等比数列{an}满足an>0(n∈N*),且a5a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+log2a5+…+log2a2n-1等于( )
A．(n+1)2
B．n2
C．n(2n-1)
D．(n-1)2
答案
答案：B
由等比数列的性质可知a5a2n-5=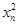
,
又a5a2n-5=22n,所以an=2n.
又log2a2n-1=log222n-1=2n-1,
所以log2a1+log2a3+log2a5+…+log2a2n-1=1+3+5+…+(2n-1)=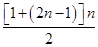 
=n2,故选B.