问题
问答题
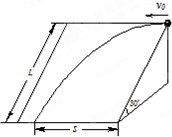
如图所示,有一倾角为30°的光滑斜面,斜面长l为10m,一小球从斜面顶端以10m/s的速度沿水平方向抛出,求:
(1)小球沿斜面滑到底端的时间t和水平位移S;
(2)小球到达斜面底端时的速度大小.(g取10m/s2).
答案
(1)在斜面上小球沿v0方向做匀速运动,
垂直v0方向做初速度为零的匀加速运动.
由牛顿第二定律得:ma=mgsin30°,
小球的加速度a=gsin30°=5m/s2,
沿v0方向位移s=v0t,
垂直v0方向:l=
at2,1 2
解得,运动时间:t=
=2l gsin300
s=2s,2×10 10×0.5
水平位移:s=v0
=102l gsin300
m=20m;2×10 10×0.5
(2)设小球运动到斜面底端时的速度为v,
由动能定理得:mglsin300=
mv2-1 2
m1 2
,v 20
小球到达斜面底端时的速度v=
=
+ghv 20
m/s=14.1m/s.102+10×10
答:(1)小球沿斜面滑到底端的时间为2s,水平位移为20m.
(2)小球到达斜面底端时的速度大小为14.1m/s.
