问题
选择题
已知等比数列{an}的公比为q,记bn=am(n-1)+1+am(n-1)+2+…+am(n-1)+m,cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m(m,n∈N*),则以下结论一定正确的是( )
A.数列{bn}为等差数列,公差为qm
B.数列{bn}为等比数列,公比为q2m
C.数列{cn}为等比数列,公比为qm2
D.数列{cn}为等比数列,公比为qmm
答案
答案:C
等比数列{an}的通项公式an=a1qn-1,
所以cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m
=a1qm(n-1)·a1qm(n-1)+1·…·a1qm(n-1)+m-1
=a1mqm(n-1)+m(n-1)+1+…+m(n-1)+m-1
=a1mq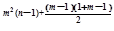 =a1mq
=a1mq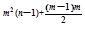 .
.
因为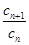 =
=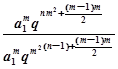 =qm2,
=qm2,
所以数列{cn}为等比数列,公比为qm2.
