问题
解答题
设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N﹡.
(1)求a1的值;
(2)求数列{an}的通项公式.
答案
(1)1 (2)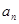 =
=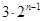
(1)令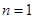 得: a1的值为1;(2)当
得: a1的值为1;(2)当 时,Tn-1=2Sn-1-(n-1)2,所以两式相减得:
时,Tn-1=2Sn-1-(n-1)2,所以两式相减得:
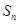 =
=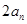 -
- ,此式对
,此式对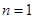 也成立,所以对n∈N﹡,都有
也成立,所以对n∈N﹡,都有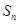 =
=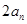 -
- ,所以)当
,所以)当 时,
时,  =
= -
- ,此两式相减得:
,此两式相减得: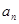 =
=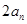 -
- -2,即
-2,即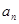 +2=
+2= ,所以
,所以
数列 是公比为2的等比数列,首项为3,所以
是公比为2的等比数列,首项为3,所以
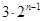 ,解得
,解得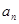 =
=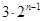 .
.
