问题
解答题
在等比数列{an}中,a2a3=32,a5=32.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,求S1+2S2+…+nSn.
答案
(1) an=2n (2) (n-1)2n+2+4-n(n+1)
解:(1)设等比数列{an}的首项为a1,公比为q,依题意得
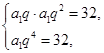
解得a1=2,q=2,
∴an=2·2n-1=2n.
(2)∵Sn表示数列{an}的前n项和,
∴Sn=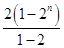
=2(2n-1),
∴S1+2S2+…+nSn=2[(2+2·22+…+n·2n)-(1+2+…+n)]=2(2+2·22+…+n·2n)-n(n+1),
设Tn=2+2·22+…+n·2n①
则2Tn=22+2·23+…+n·2n+1②
①-②,得-Tn=2+22+…+2n-n·2n+1
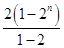=-n·2n+1
=(1-n)2n+1-2,
∴Tn=(n-1)2n+1+2,
∴S1+2S2+…+nSn=2[(n-1)2n+1+2]-n(n+1)
=(n-1)2n+2+4-n(n+1).