问题
填空题
在等比数列{an}中,an>0,且a1·a2…a7·a8=16,则a4+a5的最小值为 .
答案
2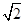
在等比数列中,由a1·a2…a7·a8=16,
得(a4a5)4=16,
所以a4a5=2,又an>0,
所以a4+a5≥2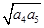
=2,
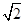当且仅当a4=a5时,取等号,所以a4+a5的最小值为2.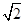
搜题请搜索小程序“爱下问搜题”
在等比数列{an}中,an>0,且a1·a2…a7·a8=16,则a4+a5的最小值为 .
2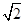
在等比数列中,由a1·a2…a7·a8=16,
得(a4a5)4=16,
所以a4a5=2,又an>0,
所以a4+a5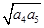≥2=2,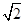
当且仅当a4=a5时,取等号,所以a4+a5的最小值为2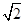.