(1) t=1    (2) T_n=+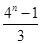

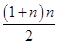
解:(1)∵点(S_n,a_n+1)在直线y=3x+1上,

∴a_n+1=3S_n+1,a_n=3S_n-1+1(n>1),

a_n+1-a_n=3(S_n-S_n-1)=3a_n,

∴a_n+1=4a_n,

a₂=3S₁+1=3a₁+1=3t+1,

∴当t=1时,a₂=4a₁,数列{a_n}是等比数列.

(2)在(1)的结论下,a_n+1=4a_n,a_n+1=4ⁿ,

b_n=log₄a_n+1=n,

c_n=a_n+b_n=4^n-1+n,

T_n=c₁+c₂+…+c_n

=(4⁰+1)+(4¹+2)+…+(4^n-1+n)

=(1+4+4²+…+4^n-1)+(1+2+3+…+n)

=+.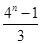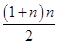