已知数列{an}成等比数列,且an>0.
(1)若a2-a1=8,a3=m.
①当m=48时,求数列{an}的通项公式;
②若数列{an}是唯一的,求m的值;
(2)若a2k+a2k-1+ +ak+1- (ak+ak-1+ +a1 )=8,k∈N*,求a2k+1+a2k+2+ +a3k的最小值.
(1)①an=8(2-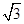 )(3+
)(3+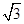 )n-1,或an=8(2+
)n-1,或an=8(2+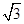 )(3-
)(3-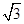 )n-1,②an=2n+2..(2)32..
)n-1,②an=2n+2..(2)32..
题目分析:(1)①确定等比数列通项,只需确定首项及等比,这需两个独立条件.由a2-a1=8,a3=m=48,得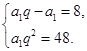 解之,得
解之,得 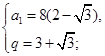 或
或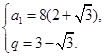 所以数列{an}的通项公式为an=8(2-
所以数列{an}的通项公式为an=8(2-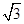 )(3+
)(3+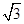 )n-1,或an=8(2+
)n-1,或an=8(2+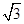 )(3-
)(3-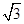 )n-1.②正确理解数列{an}是唯一的的含义,即关于a1与q的方程组
)n-1.②正确理解数列{an}是唯一的的含义,即关于a1与q的方程组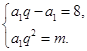 有唯一正数解,即方程8q2-mq+m=0有唯一解.由△=m2-32m=0,a3=m>0,所以m=32,此时q=2.经检验,当m=32时,数列{an}唯一,其通项公式是an=2n+2.(2)由a2k+a2k-1+ +ak+1- (ak+ak-1+ +a1 )=8,得a1(qk-1)(qk-1+qk-2+ +1)=8,且q>1.a2k+1+a2k+2+ +a3k=a1q2k(qk-1+qk-2+ +1) =
有唯一正数解,即方程8q2-mq+m=0有唯一解.由△=m2-32m=0,a3=m>0,所以m=32,此时q=2.经检验,当m=32时,数列{an}唯一,其通项公式是an=2n+2.(2)由a2k+a2k-1+ +ak+1- (ak+ak-1+ +a1 )=8,得a1(qk-1)(qk-1+qk-2+ +1)=8,且q>1.a2k+1+a2k+2+ +a3k=a1q2k(qk-1+qk-2+ +1) =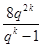 =
=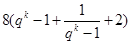 ≥32,当且仅当
≥32,当且仅当 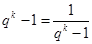 ,即q=
,即q=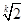 ,a1=8(
,a1=8(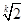 -1)时,a2k+1+a2k+2+ +a3k的最小值为32.
-1)时,a2k+1+a2k+2+ +a3k的最小值为32.
解:设公比为q,则由题意,得q>0.
(1)①由a2-a1=8,a3=m=48,得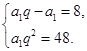
解之,得 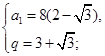 或
或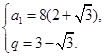
所以数列{an}的通项公式为
an=8(2-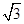 )(3+
)(3+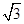 )n-1,或an=8(2+
)n-1,或an=8(2+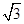 )(3-
)(3-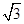 )n-1. 5分
)n-1. 5分
②要使满足条件的数列{an}是唯一的,即关于a1与q的方程组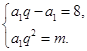 有唯一正数解,即方程8q2-mq+m=0有唯一解.
有唯一正数解,即方程8q2-mq+m=0有唯一解.
由△=m2-32m=0,a3=m>0,所以m=32,此时q=2.
经检验,当m=32时,数列{an}唯一,其通项公式是an=2n+2. 10分
(2)由a2k+a2k-1+ +ak+1- (ak+ak-1+ +a1 )=8,
得a1(qk-1)(qk-1+qk-2+ +1)=8,且q>1. 13分
a2k+1+a2k+2+ +a3k=a1q2k(qk-1+qk-2+ +1)
=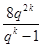 =
=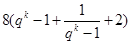 ≥32,
≥32,
当且仅当 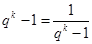 ,即q=
,即q=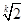 ,a1=8(
,a1=8(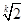 -1)时,
-1)时,
a2k+1+a2k+2+ +a3k的最小值为32. 16分
