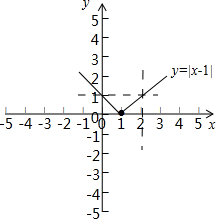
（1）因为a=1，作图如下（2分）

（2）①当a∈（-∞，1）时，f（x）=|x-a|=x-a，

因为f（x）在[1，2]递增，

所以f（x）_min=f（1）=1-a；----------（4分）

②当a∈[1，2]时，当x=a时，f（x）_min=0

③当a∈（2，+∞）时，f（x）=|x-a|=a-x，

因为f（x）在[1，2]递减，

所以f（x）_min=f（2）=a-2----------（6分）

综上所述f(x)=

1-a，a＜1 0，1≤a≤2 a-2，a＞2

----------（8分）

（3）①当x≥a时，f（x）=3x²-2ax+a²=3(x-

a

3

)2+

2

3

a²，

∴若a≥0，f（x）在[a，+∞）上单调递增，f（x）_min=f（a）=2a²；

若a＜0，f（x）在[

a

3

，+∞）上单调递增，f（x）_min=f（

a

3

）=

2

3

a²；

②当x≤a时，f（x）=x²+2ax-a²=（x+a）²-2a²，

若a≥0，f（x）在（-∞，-a]上单调递减[-a，a）上单调递增，f（x）_min=f（-a）=-2a²；

若a＜0，f（x）在（-∞，a]上单调递减，f（x）_min=f（a）=2a²；

综上f(x)min=

-2a2，a≥0 2a2 3 ，a＜0

----------（12分）