问题
解答题
（13分）（2011•重庆）设{an}是公比为正数的等比数列a1=2，a3=a2+4．
（Ⅰ）求{an}的通项公式；
（Ⅱ）设{bn}是首项为1，公差为2的等差数列，求数列{an+bn}的前n项和Sn．
答案
（Ⅰ）an=2×2n﹣1=2n（Ⅱ）2n﹣1 2n+1﹣2+n2=2n+1+n2﹣2
题目分析：（Ⅰ）由{an}是公比为正数的等比数列，设其公比，然后利用a1=2，a3=a2+4可求得q，即可求得{an}的通项公式
（Ⅱ）由{bn}是首项为1，公差为2的等差数列 可求得bn=1+（n﹣1）×2=2n﹣1，然后利用等比数列与等差数列的前n项和公式即可求得数列{an+bn}的前n项和Sn．
解：（Ⅰ）∵设{an}是公比为正数的等比数列
∴设其公比为q，q＞0
∵a3=a2+4，a1=2
∴2×q2="2×q+4" 解得q=2或q=﹣1
∵q＞0
∴q="2"
∴{an}的通项公式为an=2×2n﹣1=2n
（Ⅱ）∵{bn}是首项为1，公差为2的等差数列
∴bn=1+（n﹣1）×2=2n﹣1
∴数列{an+bn}的前n项和Sn=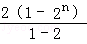
+
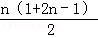=2n+1﹣2+n2=2n+1+n2﹣2
点评：本题考查了等比数列的通项公式及数列的求和，注意题目条件的应用．在用等比数列的前n项和公式时注意辨析q是否为1，只要简单数字运算时不出错，问题可解，是个基础题．