问题
解答题
将函数f（x）=x2-2|x|-1写成分段函数的形式，并在坐标系中作出他的图象，然后写出该函数的单调区间．
答案
f（x）=x2-2|x|-1=x2-2x-1x≥0 x2+2x-1x＜0
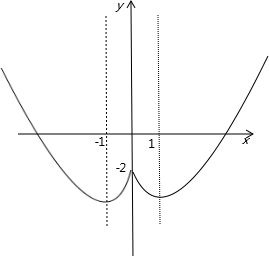
如图所示：单调增区间为（-1，0），（1，+∞）
单调减区间为（-∞，-1），（0，1）
搜题请搜索小程序“爱下问搜题”
将函数f（x）=x2-2|x|-1写成分段函数的形式，并在坐标系中作出他的图象，然后写出该函数的单调区间．
f（x）=x2-2|x|-1=x2-2x-1x≥0 x2+2x-1x＜0
如图所示：单调增区间为（-1，0），（1，+∞）
单调减区间为（-∞，-1），（0，1）