（1）a_n=2n-1(n∈N^*)      b_n=2^n-1(n∈N^*).

（2）T_n=(2n-3)·2ⁿ+3(n∈N^*)

(1)因为{a_n}是等差数列,且a₃=5,a₇=13,设公差为d.

所以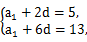解得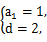

所以a_n=1+2(n-1)=2n-1(n∈N^*).

在{b_n}中,因为当n=1时,b₁=2b₁-1,所以b₁=1.

当n≥2时,由S_n=2b_n-1及S_n-1=2b_n-1-1可得b_n=2b_n-2b_n-1,所以b_n=2b_n-1.

所以{b_n}是首项为1公比为2的等比数列,

所以b_n=2^n-1(n∈N^*).

(2)c_n=a_nb_n=(2n-1)·2^n-1,

T_n=1+3×2+5×2²+…+(2n-1)×2^n-1　①

2T_n=1×2+3×2²+5×2³+…+(2n-3)·2^n-1+(2n-1)·2ⁿ②

①-②得

-T_n=1+2×2+2×2²+…+2×2^n-1-(2n-1)·2ⁿ

=1+2×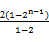-(2n-1)·2ⁿ

=1+4(2^n-1-1)-(2n-1)·2ⁿ=-3-(2n-3)·2ⁿ,

所以T_n=(2n-3)·2ⁿ+3(n∈N^*).