问题
解答题
正实数数列{an}中，a1=1，a2=5，且{an2}成等差数列。
（I）证明数列{an}中有无穷多项为无理数；
（Ⅱ）当n为何值时，an为整数，并求出使an<200的所有整数项的和。
答案
解：（Ⅰ）由已知有an2=1+24（n-1），从而an=
取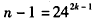
，则
用反证法证明这些an都是无理数
假设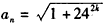
为有理数，则an必为正整数，且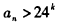
故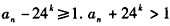
与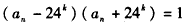
矛盾
所以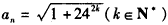
都是无理数
即数列{an}中有无穷多项为无理数；
（Ⅱ）要使an为整数，由（an-1）（an+1）=24（n-1）可知an-1，an+1同为偶数，且其中一个必为3的倍数
所以有an-1=6m或an+1=6m
当an=6m+1时，有an2=36m2+12m+1=1+12m（3m+1） （m∈N），又m（3m+1）必为偶数，所以an=6m+1（m∈N）满足an2=1+24（n-1）
即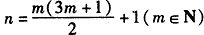
时，an为整数
同理an=6m-1（m∈N*）有a2n=36m2-12m+1=1+12m· （3m-1）（m∈N*）
也满足an2=1+24（n-1）
即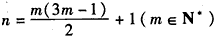
时，an为整数
显然an=6m-1（m∈N*）和an=6m+1（m∈N）是数列中的不同项
所以当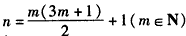
和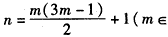
N*）时，an为整数
由an=6m+1<200（m∈N）有0≤m≤33
由an=6m-1<200（m∈N*）有1≤m≤33
设an中满足an<200的所有整数项的和为S，则
S=（5+11+…+197）+（1+7+13+…+199）
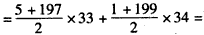6733。