问题
解答题
已知等差数列{an}满足a4=6，a6=10，
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)设等比数列{bn}各项均为正数，其前n项和Tn，若a3=b2+2，T3=7，求Tn．
答案
解：(Ⅰ)设等差数列{an}的公差为d，首项为a1，
∵
，
∴
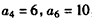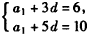，解得：
，
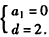∴数列{an}的通项公式an=a1+(n-1)d=2n-2。
(Ⅱ)设各项均为正数的等比数列{bn}的公比为q(q＞0)，
由an=2n-2，a3=2×3-2=4，
∵a3=b2+2，
∴b2=2，
∴
，
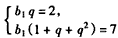解得：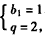
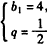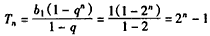或
，
∴
或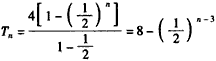
。