问题
解答题
数列{an}是首项为23,公差为整数的等差数列,且第6项为正,第7项为负.
(1)求数列的公差;
(2)求前n项和Sn的最大值;
(3)当Sn>0时,求n的最大值.
答案
解:(1)由已知a6=a1+5d=23+5d>0,a7=a1+6d=23+6d<0,
解得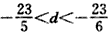 ,
,
又 d∈z,
∴d=-4。
(2)∵d<0,
∴{an}是递减数列,
又a6>0,a7<0,
∴当n=6时,Sn取得最大值,此时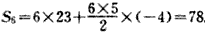 。
。
(3)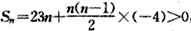 ,
,
整理得n(50-4n)>0,
∴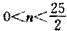 ,
,
又n∈N*,
所以n的最大值为12.
