问题
解答题
已知数列{f(n)}的前n项和为Sn,且Sn=n2+2n。
(1)求数列{f(n)}的通项公式;
(2)若a1=f(1),an+1=f(an)(n∈N*),求证:数列{an+1}是等比数列,并求数列{an}的前n项和Tn。
答案
解:(1)当n≥2时,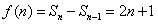 ;
;
当n=1时,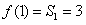 符合上式,
符合上式,
∴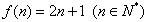 。
。
(2)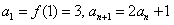 ,
,
即 ,
,
∴数列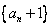 是首项为4,公比为2的等比数列,
是首项为4,公比为2的等比数列,
∴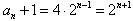 ,
,
∴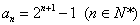 ,
,
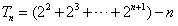
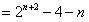 。
。
已知数列{f(n)}的前n项和为Sn,且Sn=n2+2n。
(1)求数列{f(n)}的通项公式;
(2)若a1=f(1),an+1=f(an)(n∈N*),求证:数列{an+1}是等比数列,并求数列{an}的前n项和Tn。
解:(1)当n≥2时,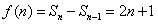 ;
;
当n=1时,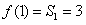 符合上式,
符合上式,
∴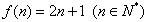 。
。
(2)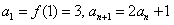 ,
,
即 ,
,
∴数列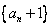 是首项为4,公比为2的等比数列,
是首项为4,公比为2的等比数列,
∴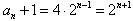 ,
,
∴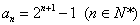 ,
,
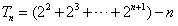
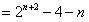 。
。