问题
填空题
设实数a1，a2，a3，a4是一个等差数列，且满足1<a1<3，a3＝4.若定义bn＝{2an}，给出下列命题：(1)b1，b2，b3，b4是一个等比数列；(2)b1<b2；(3)b2>4；(4)b4>32；(5)b2·b4＝256.其中真命题的个数为________．
答案
4
若{an}是公差为d的等差数列，则{2an}是公比为2d的等比数列，故(1)正确；a3>a1⇒公差d>0⇒公比2d>1，(2)正确；a1＋a3＝2a2，由1<a1<3，a3＝4，得a1＋a3>5⇒a2>2⇒b2＝2a2>4，(3)正确；1<a1<3，a3＝4，又a3＝a1＋2d⇒d＝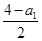
∈(
，
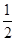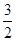)⇒a4∈(
，
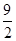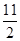)，故b4＝2a4不一定大于32，(4)不正确；因为b2·b4＝b32＝(2a3)2＝256，所以(5)正确．