问题
解答题
在数列{an}中，已知a1=8，a4=2，且满足an+2-2an+1+an=0(n∈N*)．
(1)求数列{an}的通项公式；
(2)设Sn=|a1|+|a2|+…+|an|，求Sn．
答案
解：(1)∵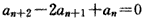
，
∴
，
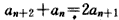∴{an}是等差数列，
设{an}的公差为d，则a4-a1=3d=2-8=-6，d=-2，
∴an=10-2n．
(2)由(1)可得{an}的前n项和为Tn=9n-n2，an=10-2n，
令bn=|an|，
当n≤5时，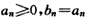
；
当n≥6时，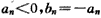
；
∴当n≤5时，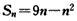
；当n≥6时，
。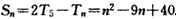