如图所示，小球在光滑斜面上做匀减速直线运动，途中依次经过A、B

问题问答题

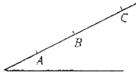
如图所示，小球在光滑斜面上做匀减速直线运动，途中依次经过A、B、C三点，且经过两段的时间间隔分别为t_AB=1s，t_BC=3s，且AB=4m，BC=6m，求：

（1）小球的加速度；

（2）小球通过C点的速度；

（3）小球能沿斜面上滑最大的距离．

答案

（1）设小球在斜面上运动的加速度为a，经过A点时的速度为v_A，那么有：

v_B=v_A+at_AB… ①

=2aSAB… ②

v_C=v_A+a（t_AB+t_BC）… ③

=2a(SAB+SBC)… ④

联立①②式得：(vA+atAB)2-

=2aSAB… ⑤

联立③④式得：[vA+a(tAB+tBC)]2-

=2a(sAB+sBC)… ⑥

联立⑤⑥式代入数据解之得：a=-1m/s²，v_A=4.5m/s

（2）由式③有：v_C=v_A+a（t_AB+t_BC）=4.5+（-1）×（1+3）m/s=0.5m/s

（3）设小球沿斜面上滑最大距离为s_m，根据速度位移关系式v2-

=2asm有：

sm=

0-(4．5)2

2×(-1)

m=10.125m

答：（1）小球的加速度a=-1m/s²；

（2）小球通过C点的速度v_C=0.5m/s；

（3）小球能沿斜面上滑最大的距离为10.125m．